Quadratic Equation class 10 notes|class 10 Maths chapter 4 notes|CBSE class 10 Maths notes |
QUADRATIC EQUATIONS
Topics to be covered:
- Quadratic Polynomial.
- Quadratic equation.
- Types of quadratic equation.
- Roots of a quadratic equation.
- Methods for solving the quadratic equation.
- Nature of roots.
- A polynomial of degree 2 is known as Quadratic polynomial.
- It is in the form of P(x)=ax2+bx+c, a≠0
- A quadratic equation in the variable x is an equation of the form ax2+bx+c, where a, b and c are real numbers and a≠0 is called a quadratic equation.
- Standard form-ax2+bx+c.
- Complete quadratic equation-ax2+bx+c,where a, b and c are real numbers and a≠0 .
- Pure quadratic equation-ax^2=0.
METHODS TO SOLVE THE QUADRATIC EQUATION
There are three methods for solving quadratic equation:
(a) By factorization
(b) By completing the square
(c) By Quadratic Formula
(A) Factorisation Method:
-In this method we factorise the equation into two linear factor and equate each factor to zero to find the root of the given equation.
Step 1 - Given quadratic equation in the form of ax2+bx+c.
Step 2- split the middle term BX as MX + NX so that the sum of m and n is equal to (b) and sum of product of n and m is equal to a×c.
Step 3- by Factorisation we get two linear factors (x+p)and (x+q).
Step 4- Now we have to equate fector to zero to find the value of x.
Example-
x2 – 3x – 10 = 0
⇒ x2 - 5x + 2x - 10 = 0
⇒ x(x - 5) + 2(x - 5) = 0
⇒ (x - 5)(x + 2) = 0
Roots of this equation are the values for which (x - 5)(x + 2) = 0∴ x - 5 = 0 or x + 2 = 0⇒ x = 5 or x = -2
(B) COMPLETING THE SQUARE METHOD
-In this method we convert the equation in the square form of(x + a)2 — b2 = 0 to find the roots.
Step 1- We have given a quadratic equation in the form of ax2+bx+c.
Step 2- Divide the quadratic equation by the coefficient of x square. i.e a.
Step 3- Transfer the constant on RHS then add square of the half of the coefficient of x to both sides.
Step 4- Now write lhs perfect square and simplifies the RHS.
Step5- Take the square root on RHS-
-Based on the value of the discriminant, D=b2−4ac, the roots of a quadratic equation can be of three types.
Case 1: If D>0, the equation has two distinct real roots.
Case 2: If D=0, the equation has two equal real roots.
Case 3: If D<0, the equation has no real roots [ Imagery Roots].
Also visit related links
Chapter : Quadratic Equation
- HANDRITTEN NOTES
- NCERT SOLUTIONS
- NCERT EXAMPLER
- CASE STUDY
- PYQs



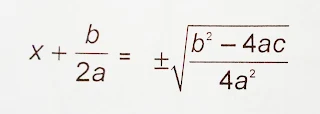








Post Comment